Защита информации
в компьютерных системах

y^2 = x^3 + ax + b mod p (обозначается, как нормальная форма Вейерштрасса)

    Кроме того, вышеуказанное уравнение подчиняется следующему ограничению:

4a^3 + 27b^2 != 0 mod p

    Таким образом, эллиптические кривые состоят из точек:(x,y):

y^2=x^3+ ax + b mod p, которые симметрично расположены относительно x-оси.

    Кроме того, мы добавим дополнительную точку, I, которая представляет собой точку на бесконечности.
Итак, у нас имеется конечное множество решений этого уравнения, с p + t + 1 парами точек, где |t|<=sqrt(p).
    Другими словами, точки на эллиптической кривой формируют конечное абелево множество и могут таким образом использоваться подобным способом для полей и всего такого. Теперь определим основные операции на этом множестве.

    Эллиптическая кривая, состоящая более чем из одного "сегмента" (многосвязная).

    Можно видеть процесс сложения точек P и Q (также, как R + R), объясняемый ниже. Обратите внимание на специальную точку I и вертикальную линию, соединяющую ее и точки S и -S.
    Сложение определяется следующим образом: сумма P + Q, где P и Q - точки где-нибудь на кривой, является {\it отражением} третьей точки кривой, которой касается (или которую пересекает) линия, соединяющая P и Q (по существу, используются касательные и хорды; смотри рисинок).

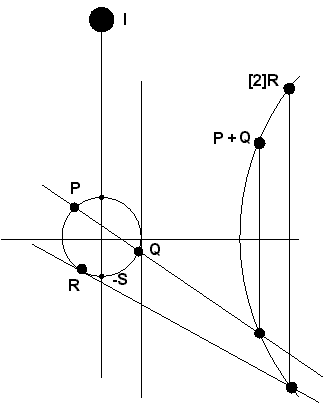
    Если P и Q - одна и та же точка ( скажем, P = Q = R ), то сумма записывается [2]R (или, более просто, 2R ), где линия, "соединяющая" две точки R - просто касательная к кривой в точке R. Поскольку I - на бесконечности, линия, соединяющая P и I, вертикальна и просто пересекает эллиптическую кривую, давая отражение P (-P). Таким образом, отражение этой точки (-P) - просто P; и, эффективно, I - выполняет функцию идентичности для этого конечного множества. Эквивалентно, если линия, соединяющая точки P и Q вертикальна ( Q = -P ), то их сумма равна I, поскольку эта линия снова "касается" эллиптической кривой в точке на бесконечности.
    Более формально, определим сложение с помощью геометрии, вычисляя уравнение для линии между P и Q как

$y=lambda*x + beta,

находя третью точку пересечения между эллиптической кривой и этой линией, и последовательно взяв отражение этой точки в качестве суммы. Следующий алгоритм обрисовывает эту процедуру:

Дано: P =x_1,y_1, Q = x_2,y_2,

если (x_1= x_2)&(y_1 = -y_2), то (P+I):= I(Q=-P).

если (x_1= x_2), то lambda = (3x_1^2 + a)/(2y_1) mod p,

(где lambda - наклон, т.е. эта формула получена взятием производной в точке (x_1,y_1)).

иначе lambda = (y_2 - y_1)/(x_2-x_1) mod p

Определим beta = y_1 - lambda*x_1.

Тогда, x_3 =lambda^2- x_1- x_2,

y_3 =-(lambda*x_3 +beta)

P+Q := (x_3,y_3) mod p.

    Эта операция сложения - коммутативна, также как ассоциативна (что несколько удивительно; доказательство - вне возможностей этого курса ). Таким образом, мы получаем систему, где мы можем определить сложение аналогично умножению по модулю p.

    Мы используем следующую нотацию для этого множества чисел.

E_n(a,b) = множество точек эллиптической кривой,которые удовлетворяют:

-y^2 = x^3 + ax + b

-gcd(4a^3+27b^2,n) =1

плюс содержит специальную точку I.

E_p, для простого p, представляет эллиптическую группу

N_p(a,b) = порядок E_p(a,b).

O(E_p)(M) = порядок элемента M в E_p.

    Итак, теперь, вместо умножения, мы используем операцию сложения, определенную выше. Последовательным образом, вместо вычисления степени по модулю g^k mod p, мы "умножаем" P (эквивалент g в этом эллиптическом царстве) на k(=[k]P),определяя, как: P + P + P + P. .. + P (k раз). Это делает "дискретную проблему логарифма" эквивалентной обнаружению того, сколько раз точка P должна быть добавлена к себе, чтобы равняться другой точке Q.

Эллиптические кривые&&Эль-Гамаль

Мы можем сделать точки P и Q = [k] P открытыми, пока держим k в секрете; это полностью аналогично работе с модулем p. Однако, теперь некоторые "уловки" с дискретными логарифмами больше не работают, что эффективно позволяет нам использовать более короткие ключи, делающие в целом более быстрыми криптографические алгоритмы и их выполнение.